1. Между населенными пунктами A,B,C,D,E,Fпостроены дороги, протяженность которых приведена в таблице(отсутствие числа означает, что прямой дороги нет). Определить длину кратчайшего пути между пунктами E и F. (Передвигаться можно только по построенным дорогам).

Решение:
В этом задании исходные данные представлены в виде таблицы, которую можно рассматривать как матрицу неориентированного взвешенного графа. Вершинами данного графа являются населенные пункты A,B,C,D,E,F. Элементы данной матрицы показывают, какие населенные пункты связаны дорогами и какова их длина.
Для более наглядного представления изобразим данные таблицы в виде графа. Для этого в произвольном порядке изображаем вершины, затем соединяем их ребрами и указываем вес каждого ребра. Нам надо указать длину кратчайшего пути из пункта А в пункт F.  Нарисуем этот путь с конца.

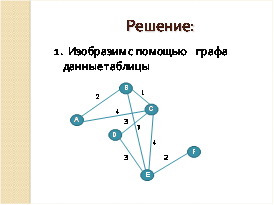
Сначала изобразим конечный пункт F. В этот пункт можно попасть только из пункта Е. Соединяем пункты Е и F  дугой и указываем вес этой дуги. Он равен двум, то есть расстоянию между пунктами  Е и F. Соответственно по графу можно увидеть, что в пункт Е можно попасть  из пунктов B, C и D. В пункт В можно попасть из А. В пункт С – из В и А. В  пункт D – из С. В пункт В попадаем из А. В пункт С – из В и А. И в пункт В из А.

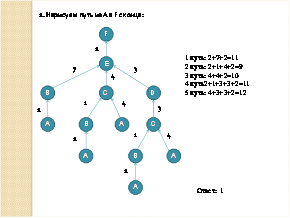
Данную схему можно рассматривать как ориентированный взвешенный граф, который наглядно показывает, что есть 5 путей из пункта А в пункт F. Подсчитываем длину каждого пути 
1 путь: 2+7+2=11;
2 путь: 2+1+4+2=9;
3 путь: 4+4+2=10;
4 путь2+1+3+3+2=11;
5 путь: 4+3+3+2=12. 
Так как нам надо определить длину кратчайшего пути, то выбираем второй путь, длина которого равна 9. Данный ответ находится под цифрой 1. Поэтому в ответе надо поставить крестик в клеточке, соответствующей первому ответу.

2. У исполнителя Утроитель две команды, которым присвоены номера
1. Прибавь 1;
2. Умножь на 3.
Запишите порядок команд в программе преобразования числа 1 в число 22, содержащей не более 5 команд.
Решение:
Для решения данного задания используем метод от обратного, то есть будем преобразовывать число 22 в 1. Соответственно команды исполнителя заменим командами антагонистами, то есть команду «Прибавь 1» заменим командой «Вычти 1», а «Умножь на 3» заменим командой «Раздели на 3». Ход выполнения команд можно изобразить в виде  дерева, каждая вершина которого имеет две ветки, соответствующие командам 1 и 2. Корнем этого дерева является число 22. Это дерево будет иметь 5 ярусов, так как программа должна содержать не более 5 команд. Но здесь нужно учесть один момент. Если число  делится на 3, то вершина будет иметь 2 потомка, а если нет, то одного (то есть делить на 3 мы не можем, а можем только вычитать 1). Получаем следующее дерево.

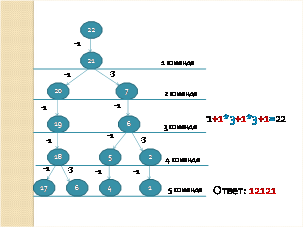
 Инвертируем теперь команды и преобразуем число 1 в 22.
    1+1*3+1*3+1=22.
   Учитывая номера команд, записываем программу решения данной задачи в виде  последовательности соответствующих команд. Ответ: 12121

 
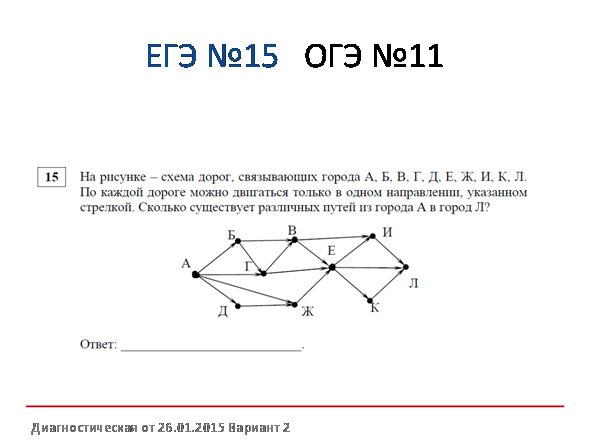
Решение: (1 способ)
Условие данного задания представлено в виде ориентированного графа, вершинами которого являются названия городов, а дороги, соединяющие эти города, являются дугами графа. Для того, чтобы решить данную задачу, построим еще один ориентированный граф, но с  учетом того, по каким дорогам можно будет попасть в пункт Л.

 По графу легко подсчитать количество дорог, ведущих из города А в город Л.
 

3.У Исполнителя Кузнечик 2 команды:
1. Прибавь 3;
2. Вычти 2.
Сколько различных чисел можно получить из числа 1 с помощью программы, которая содержит ровно 5 команд. 
Решение:
Оформим решение данной задачи в виде дерева, вершинами которого будут являться числа, соответствующие промежуточным значениям. Данное дерево будет иметь корень, равный 1 и 5 ярусов, так как у нас должно быть ровно 5 команд.

 4. У исполнителя Устроитель две команды, которым присвоены номера:
1. Прибавь 1;
2. Умножь на 3.
Программа для Устроителя – это последовательность команд. 
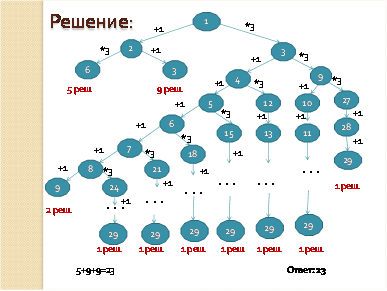
Сколько есть программ, которые преобразуют 1 в число 29?

  При решении данной задачи следует учитывать, что если число больше 9, то умножать на 3 мы не можем, так как получится число, большее 29, следовательно, вершины с числами большими 9 будут иметь только одну ветвь, соответствующую команде +1.

5.Даны три кучи камней, содержащих соответственно 2, 3, 4 камня. За один ход разрешается или удвоить количество камней в какой-нибудь куче, или добавить по 2 камня в каждую из всех трех куч. Выигрывает тот, после чьего хода в какой-нибудь куче становится больше или равно 15 камней или во всех трех кучах суммарно становится больше либо равно 25 камней. Игроки ходят по очереди. Выяснить, кто выигрывает при правильной игре – первый или второй игрок? 
Решение:    В разумной партии каждый игрок должен стараться следовать общему правилу – всегда оставлять противнику проигрышную позицию. В ходе решения задач можно заметить, что в одной партии в Камешки только один из игроков может следовать этому правилу – тот, кто первым может занять выигрышную позицию (имеет выигрышную стратегию). Если он будет ей следовать, а, значит, делать только разумные ходы и оставлять противнику только проигрышные позиции, то выиграет при любой игре противника. Если начальная позиция выигрышная, то выигрышную стратегию имеет Первый, если проигрышная – Второй.  
Изобразим решение данной задачи в виде графа.

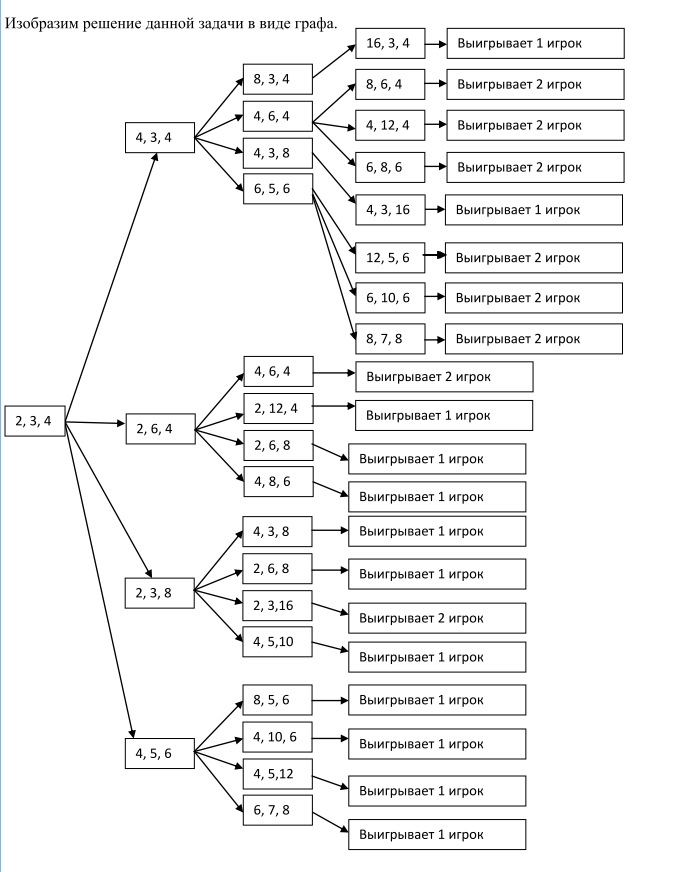
Ответ:  при правильной стратегии игры выигрывает первый игрок. При этом первый его ход должен быть 2, 3, 4                 4, 5, 6.

Литература: 
ФИПИ (открытый банк данных)
Материалы демонстрационных вариантов ЕГЭ по информатике  2016, 2015 года
Материалы диагностической работы 2015 года.